RF 관점에서의 L과 C

L과 C를 이해하기 위해서는

대상용어의 정의를 이해하면 일단 반은 먹고 들어가는 겁니다. 하지만 L과 C라는 개념은, 단순히 정의로 파악하고 이해할 수 있는 대상이 아닙니다. 실제 활용상의 특성과 현상으로 습득해야 하는 문제입니다.

먼저 Inductance와 Capacitance는 서로 반대되는 현상을 말합니다. 그러므로 L과 C는 정 반대의 특성과 현상을 보인다는 점을 미리 명심할 필요가 있습니다. 우선 관련 용어들의 고전적인 정의부터 정리해보겠습니다.

☞ Inductance (인덕턴스 , 유도용량) : 회로를 흐르고 있는 전류의 변화에 의해 전자기유도로 생기는 역(逆)기전력의 비율을 나타내는 양. 단위는 H(헨리)이다. 이러한 인덕턴스 값을 간단히 L 이라 지칭하며, RF에선 nH단위가 주로 사용된다.  ☞ Inductor (인덕터) : 인덕턴스를 일으키는 소자 또는 구조물  ☞ Coil (코일) : 인덕턴스는 선로길이가 길 때 나타나는 현상이므로 선로를 스프링모양으로 감으면 적은 면적상에 많은 인덕턴스를 구현할 수 있다. 또한 상호 인덕턴스가 강해져서 선로길이보다 더 많은 인덕턴스를 구현현할 수 있다. 주로 저주파에서 사용되는 용어로서, 고주파에서는 이런 코일 구조뿐 아니라 다양한 구조가 응용되기 때문에 코일이란 용어는 별로 안쓰고 인덕터라는 용어를 주로 사용한다.

☞ Capacitance (캐패시턴스 , 정전용량)  전압을 가했을 때 축적되는 전하량의 비율을 나타내는 양. 단위는 F(패럿)이다. 이러한 캐패시턴스 값을 간단히 C 라 지칭하며, RF에선 pF 단위가 주로 사용된다.  ☞ Capacitor (캐패시터) : 캐패시턴스를 일으키는 소자 또는 구조물  ☞ Condensor (콘덴서) : 주로 저주파에서 사용되는 용어로서, nF ~ mF 수준 이상의 큰 캐패시턴스값을 가지는 소자를 콘덴서라 부르는 경향이 있다. 같은 의미지만 작은 C값을 사용하는 RF에서는 캐패시터란 용어를 주로 사용한다.

실제로 L과 C는 꽤 다양한 범위에서 설명이 가능합니다. 위의 설명은 그냥 그런다 보다 하고 넘어가고, 우리가 진짜 알아야 할 핵심은 바로 RF에서의 L과 C의 의미를 정확히 이해하는 것입니다.

L과 C의 주파수 특성

저 위에 사전적으로 정의된 내용으로는 솔직히 주파수 특성을 정확히 판단할 수 없습니다.

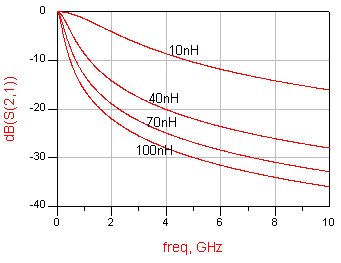
그럼 이제 완전히 RF적인 관점에서 L과 C의 S21 투과 특성을 살펴보도록 하겠습니다. 수동소자이므로 S21이 0dB에 가까울수록, 즉 위로 올라붙을수록 신호가 손실없이 통과된다는 뜻이란건 다 아시죠?

캐패시터의 S파라미터

왼쪽은 캐패시터(C)의 주파수 특성 중 S21 즉 주파수 통과 특성을 보여준 그래프입니다. 인덕터와는 정 반대로 주파수가 낮을수록 잘 통과하지 못하고 있습니다. 그리고 C값이 높아질수록 저주파는 물론 고주파 성분이 더 많이 통과하고 있습니다.

캐패시터는 (C값에 따라) 고주파 신호를 더 잘 통과해내고 있습니다.

결론 났습니다. 고주파 RF의 관점에서 L과 C라는 지표의 특성을 간결하게 정의해보겠습니다.

L (Inductance) : 주파수가 올라갈수록 얼마나 고주파의 흐름을 방해하는가?

C (Capacitance) : 주파수가 올라갈수록 얼마나 고주파의 흐름을 원활하게 하는가?

물론 이게 다는 아닙니다만, 우리가 lnductance가 존재하느니 Capacitance가 존재하느니 하는 기준은 바로 위의 특성을 통해 판단한다는 점 - 고주파가 될수록 신호를 잘 통과시키느냐, 막느냐 - 을 명심하시기 바랍니다. 

바로 이 특성에 기반하여 lnductance와 Capacitance는 상황에 따라 적절한 용도로 사용되고 있는 것입니다. 주파수를 가진 신호를 다룰 때 이 L과 C라는 요소를 적절히 사용하여 주파수 자원을 놨다가 풀었다가 함으로써 원하는 RF회로와 시스템을 구현된다는 점!

이 개념을 명확히 익히고, 이제 L과 C의 자체적인 특성을 다시 들여다 보도록 하겠습니다.

L : Inductance(인덕턴스)

lnductance L은 도선에 전류가 흐를 때 그 전류의 변화를 막으려는 성질, 또는 그 정도를 말합니다. 일종의 전기적 관성이라는 개념이라고 볼 수도 있겠지요.

즉 도선에 흐르는 전류가 직류(DC)라면 아무 변화 없이 잘 흘려주지만, 그것이 변하려고 하면 막 화를 냅니다. 결국 전류가 원래 흐르던 방향이나 크기가 바뀌려고 하면 그 반대의 기전력을 만들어서 그 변화를 막으려고 하지요.

그래서 전류/전압 파형의 크기, 방향이 주기적으로 변하는 교류(AC)가 입력되면 그 변화를 막으려고 안간힘을 쓰게 됩니다. 그래서 DC는 잘 통과하지만 AC는 좀체 통과하기 힘들 게 만드는 것이지요. 이게 무슨 원리라고 말하긴 좀 그렇고, 예전 학자들이 이러한 교류 변화의 흐름을 막고자 하는 그 성질을 Inductance로 정의했습니다.

그렇다면 이런 Inductance는 어디에서 발생할까요?

길이를 가지는 모든 선로에서 발생합니다.

그렇습니다. 아래 그림을 보시지요.

아무 선로건 그 선로 길이 방향으로 둥글게 자기장을 형성하게 되는데, 만약 이 선로를 따라 흐르던 전류가 변화하려 하면 그 주변에 생성된 자기장도 길이 바뀌어야 합니다. (오른손 법칙 다 기억하시죠?) 바로 이렇게 선로 주위에 생성된 자기장이 선로의 전류/전압 변화를 따라가려면 어느 정도 시간이 필요해집니다. 결국 자기장이 한 박자 늦게 변하려 하다 보면 결국 도선의 전류 변화를 방해하는 꼴이 되는 것이지요.

그리고 이러한 주변의 자기장이 많이 생길수록 (즉 L값이 커질수록) 전류가 변화하기가 무척 힘들 겁니다. 주변의 자기장을 일일이 설득해서 자기를 따라 변하게 해야 하는데, 그 대상이 많아질수록 쉽지 않은 것입니다. 그래서 L값이 높을수록 고주파는 통과하기 힘들어 하는 것이지요.

그렇다면 Inductancee를 유발시키는 Inductor는 어떻게 만드나요?

선로를 길게 만들면 됩니다.

아주 간단하지 않습니까? 선로만 길면 주변의 자기장은 길이만큼 점점더 늘어나니까 Inductance는 죽죽 늘어납니다. 그런데 무식하게 길게만 만들 수 없으니, 둘둘 감아서 스프링모양의 Coil로 만들게 되죠. 그래서 Coil = Inductor처럼 공식화된 것이구요.

여기서 한가지 짚고 넘어갈 것은, 이렇게 Coil 형태로 만들어 놓으면 실제 그 선로 길이만으로 구현한 것보다 L값을 증가시킬 수도 있습니다. 왜냐하면, lnductance는 Self Inductance(자기유도)와 Mutual Inductance(상호유도)가 존재하기 때문입니다.

Mutual Inductance는 위의 그림과 같이 방향에 따라 다른데, 만약 전류가 같은 방향이라면 상호간의 주변의 자기장이 서로 더해져서 L값은 더더욱 세집니다. 반면 반대로 전류가 서로 다르게 흐르고 있다면 서로간의 자기장 방향이 달라서 상쇄가 되기 때문에 전체적인 L값이 작아지는 효과가 발생합니다.

RF에서